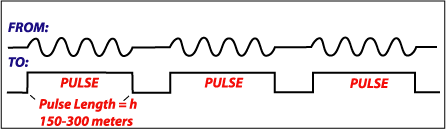
Radar Equation for Distributed Targets - The Pulse Volume

• Thus far, we've derived the radar equation for a point target.
• This will work fine if you are interested in point targets such as airplanes
• However, in a thunderstorm or some area of precipitation, we do not have just one target (e.g., raindrop), we have many.
• Thus we need to derive a radar equation for distributed targets
• Before we do so, let's learn more about the radar pulse volume

RADAR PULSE VOLUME AND RADAR RESOLUTION  

• First, let's simplify the real beam according to the diagram:

Q:  What does a "three-dimensional" segment of the radar beam look like?  ->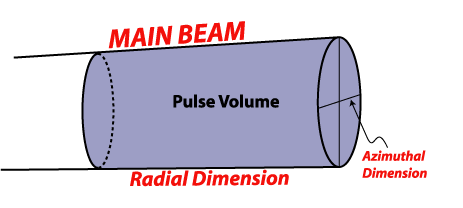 

Q:  What is the radial resolution of the pulse? 

In other words, what is the smallest radial distance that the pulse can occupy? 

HINT: remember that the pulse will be traveling out to a target, scatter off of it and then propagate back to the radar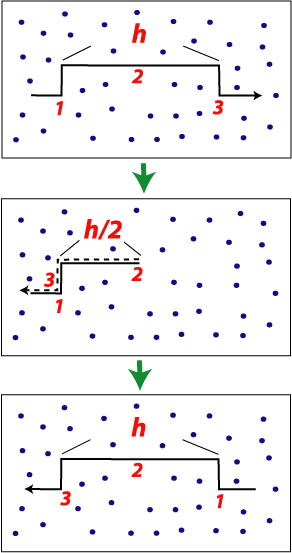

So, what is the radial resolution for a given radar?? Answer

Back to the three-dimensional pulse volume.  

What is the azimuth dimension of the pulse volume??  Answer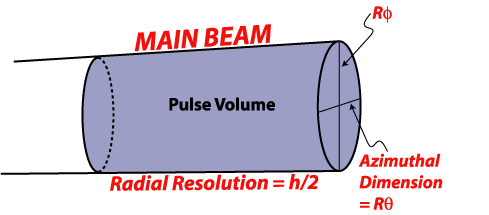

So, the "volume" of the pulse volume is:

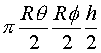
For a circular beam, then q = f, the pulse volume becomes:

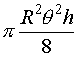
Q:  Does the pulse volume radial resolution change as you move away from the radar??  Answer

Q:  Does the pulse volume azimuth dimension change as you move away from the radar??  Answer

Q:  How does one calculate the azimuth dimension of the radar beam??  Answer

VERY IMPORTANT:

The "azimuth dimension" is not the "azimuthal resolution." 

• The azimuth dimension is the distance across the beam as determined by the half-power beam width.
• Since a radar data point is determined by many pulses, the "azimuth resolution" is also a function of the antenna rotation rate, PRF, and number of pulses used to calculate the reflectivity and Doppler velocity estimates.  Therefore, the azimuth resolution tends to be larger than the azimuth dimension. 
• Review pages 42-46 at: http://www.wdtb.noaa.gov/courses/dloc/topic3/lesson2/player.html.

Let's take a look at the pulse volume and how it changes with range with real data.......