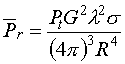 (1)
(1)
Radar Equation for Distributed Targets
- The beam is filled with targets. Q: Where/when would this assumption break down?
- Multiple scattering is ignored.
- Total average power is equal to the sum of powers scattered by individual particles.
Recall the radar equation for a single target:
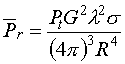 (1)
(1)
- Pr is the average received power
- Pt is the transmitted power
- G is the gain for the radar
- l is the radar's wavelength
- s is the targets scattering cross section
- r is the range from the radar to the target
For multiple targets, (1) can be written as:
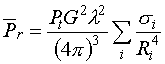 (2)
(2)
where the sum is over all targets within the pulse volume.
If we assume that h/2 << ri,
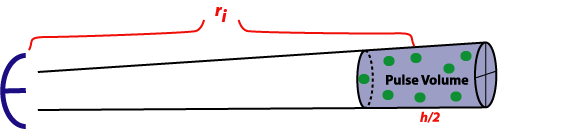
then (2) can be written as:
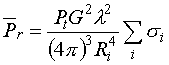 (3)
(3)
It is advantageous to sum the backscattering cross sections over a unit volume of the total pulse volume.
Hence the sum in (3) can be written as:
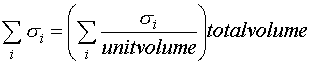 (4)
(4)
where the total volume is the volume of the pulse.
Thus, (4) can be written as:
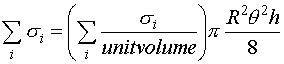 (5)
(5)
Substituting (5) into (3) gives:
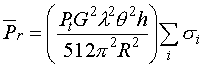 (6)
(6)
Note that:
Pr is proportional to R-2 for distributed targets
Pr is proportional to R-4 for point targets.
WHY????? Answer
RADAR REFLECTIVITY
The sum of all backscattering cross sections (per unit volume) is referred to as the radar reflectivity (h). In other words,
![]() (7)
(7)
Q: What are the units of h? Answer
In terms of the radar reflectivity, the radar equation for distributed targets (6) can be written as:
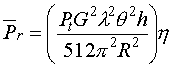 (8)
(8)
all variables in (8), except h are either known or measured.
Now, we need to add a fudge factor due to the fact that the beam shape is gaussian (we could derive this, but it's not worth the trouble. Check out the reference books if you are interested).
Hence, (8) becomes;
 (9)
(9)
COMPLEX DIELECTRIC FACTOR
The backscattering cross section (si) can be written as:
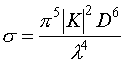 (10)
(10)
where:
- D is the diameter of the target
- l is the wavelength of the radar
- K is the complex dielectric factor
- is some indication of how good a material is at backscattering radiation
For
water,
![]() =
0.93
=
0.93
For
ice, ![]() = 0.197.
= 0.197.
Notice that the value for water is much larger than for ice. All other factors the same, this creates a 5 dB difference in returned power.
So, let's incorporate this information into the radar equation.
Recall
from (7) that
![]() .
Using (10), h
can be written as:
.
Using (10), h
can be written as:
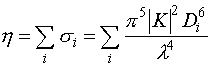 (11)
(11)
Taking the constants out of the sum;
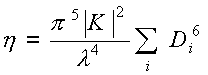 (12)
(12)
Remember that the sum is for a unit volume. Substituting (12) into (9) gives:
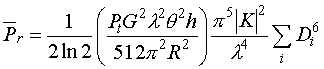 (13)
(13)
Simplifying terms gives:
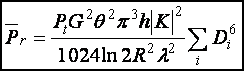 (14)
(14)
Note the Di6 dependence on the average received power.
RADAR REFLECTIVITY FACTOR
In Equation (14), all variables except the summation term, are either known or measured.
We will now defined the radar reflectivity factor, Z, as:
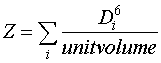 (15)
(15)
Q: What are the units of Z? Answer
Substituting (15) into (14) gives the radar equation for distributed targets:
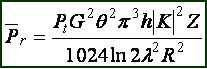 (16)
(16)
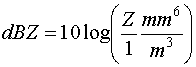 (17)
(17)