THEORY FOR GOES ORBIT
Q: Why are GOES 35,800 km from the center of
the earth so that they are in geosynchronous orbit???
There
are two relevant forces involved in this problem: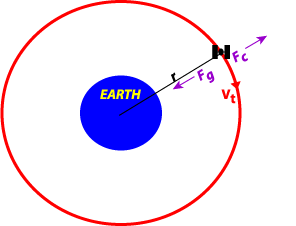
1. gravitational force of attraction between any two objects, given by:
![]()
2.
centrifugal force an outward-directed force that normally balances
the inward-directed centripital force, given by:
![]() . These forces are
required to help maintain the circular trajectory of an object.
. These forces are
required to help maintain the circular trajectory of an object.
In our situation of a satellite in geosynchronous orbit, the outward-directed centrifugal force balances the inward-directed gravitational force. Hence, for a steady-state orbit, the force balance becomes:
![]() or
or
![]() (1)
(1)
Solving
for vs, the tangential velocity of the satellite, from (1)
yields:
![]() (2)
(2)
Notice,
that in (2), the mass of the satellite does not appear.
REALITY CHECK – what are we trying to solve for?????
OK,
so what is vs?
The
tangential velocity of the satellite (vs) is related to its
orbital period, T through:
![]() or
or ![]() or
or ![]() (3)
(3)
Eliminating
![]() between (3) and (2)
gives:
between (3) and (2)
gives:
![]()
Solving
for the orbital period, T, gives:
![]() (4)
(4)
OK,
we still do not know r………but we’re getting closer. To find r, we still need to determine
what T is…..
What
is the constraint, in terms of angular velocity, on the satellite if it is to
be in a geosynchronous orbit??????
Yes,
![]() where ws and we are the angular velocities of the satellite
and earth, respectively.
where ws and we are the angular velocities of the satellite
and earth, respectively.
The
angular velocity (from basic physics) for the satellite is:
![]() (5)
(5)
but
from (3), recall that ![]() or
or ![]() (6)
(6)
Substituting
(6) into (5) gives:
![]() or solving for T,
or solving for T,
![]() or
or 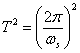 (7)
(7)
recall
that ![]() so (7) can be
rewritten as:
so (7) can be
rewritten as: 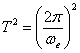 (8)
(8)
From (8), we now know the satellites orbital period, T.
By substituting (8) into (4) to eliminate T2 we get:
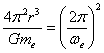 or solving for r
yields:
or solving for r
yields: 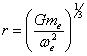 (9)
(9)
We
know:
G = 6.67 x 10-11 Nm2kg-2
me = 5.97 x 1024 kg
we = 7.29 x 10-5
rad s-1
Hence,
substituting the above constants into (9) gives:
R = 35,786 km for GOES