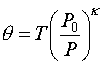
Propagation of Errors

• For variables that are directly measured (e.g., temperature, pressure, etc.) it is possible to estimate measurement uncertainty through experimentation with the instrument of interest (e.g., thermometer).

• However, not all variables of interest are directly measured with an instrument.  

• For example, how does one estimate the uncertainty of potential temperature (q) ?????

• Recall that potential temperature is given by a form of Poissons Equation:

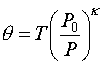
or q(T,P)

So, how do the uncertainties in T and P propagate into uncertainties in q ??

Here's the solution:

Start with Poissons Equation:

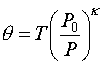  (1)

Take the ln of both sides:

  (2)

Now, let's differentiate (2),

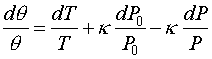      (3)

But, we know that dP_o = 0, so (3) becomes:

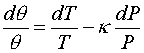       (4)

Now, let's square (4);

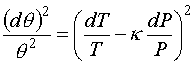  (5)

expanding out the rhs gives:

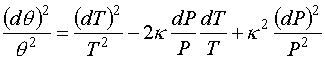  (6)

or rearranging the rhs gives,

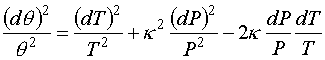  (7)

At this point, we will assume that the errors in T and P are independent of each other. 

In other words, the errors in T and P are not correlated.

Thus, the last term on the rhs of (7) is zero since it represents an error correlation term between T and P.

Hence, (7) can be written as:

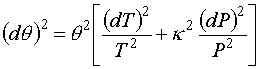  (8)

or in finite difference form;

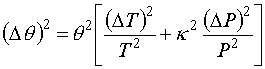  (9)

Note that (Dq)², (DT)² and (DP)² can be interpreted as variances (s²).

As you know from Statistics, s² is a measure of uncertainty.  Hence, equation (9) gives the variance, or uncertainty of potential temperature in term of the variances of T and P.

Questions?????